An ACT-R Model of Cognitive Arithmetic
Christian Lebiere
Carnegie-Mellon University
Talk Outline
Introduction
Basic ACT-R model
Activation-based declarative retrieval
Computation and conflict resolution
Error modeling
Some cognitive arithmetic effects
The problem-size effect
Errors in addition retrieval
Errors in multiplication computation
Learning
The problem-size effect over time
Analysis of cognitive dynamics
Power-law curve of retrieval odds
Influence of various factors
The lifetime simulation
A model which learns (almost) everything
Analysis tools
Sensitivity to experimental conditions
Extension of formal analysis
Conclusion
Introduction
Why Cognitive Arithmetic?
Practical task
One of the three basic Rs
Not a toy problem
Everybody does it
Reliable data across the population spectrum
Abstract task
No built-in bias
Hierarchical task
Each skill is used to learn more complex skills
Regular task
Fewer rules/exceptions than natural language
Statistics-friendly
Very hard for humans but very easy for computers
Insights into human architecture
Lessons for AI
Model: Activation-based Retrieval
![]() Bayes Equation
Bayes Equation
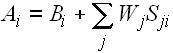
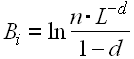 Base-Level Equation
Base-Level Equation
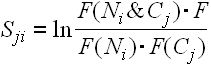 Associative Strength Equation
Associative Strength Equation
retrieval =goal> isa arithmetic first =first operator =operator second =second result nil =fact> isa arithmetic first =first operator =operator second =second result =answer ==> =goal> result =answer !pop!
|
|
Fact reinforcement upon retrieval
Fact creation or reinforcement upon goal popping
Model: Computation and Conflict Resolution
![]() Conflict Resolution Equation
Conflict Resolution Equation
![]() Latency Equation
Latency Equation
iteration =goal> isa arithmetic first =first operator plus second =second result nil ==> =subgoal> isa iterate start =first counter =second increment 1 result =answer !push! =subgoal =goal> result =answer | calculator =goal> isa arithmetic first =first operator plus second =second result failure ==> !bind! =answer (+ =first =second) =goal> result =answer |

P and C of retrieval and computation productions
Recovery from subgoal failure
Gradual switch from computation to retrieval
Model: Errors
Full Activation Equation including mismatch penalty and noise:
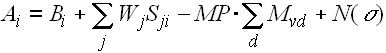
Retrieval can only be completed if activation is above the retrieval threshold RT.
The mismatch measure encodes the similarity between memory elements such as numbers.
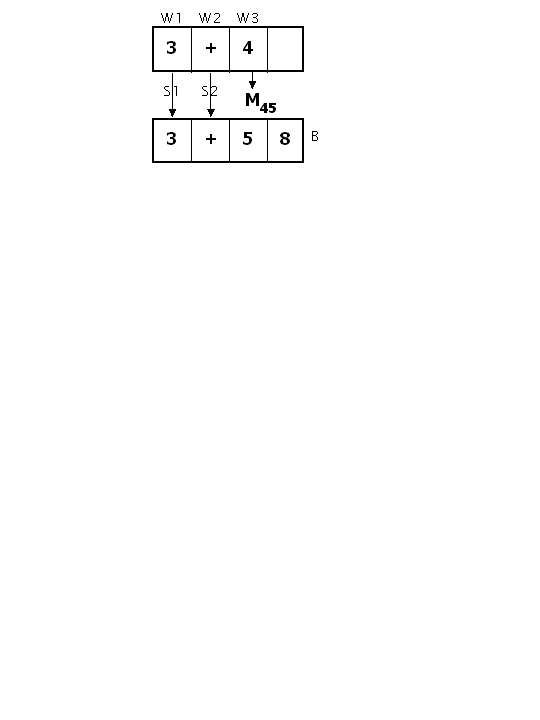
Omission: no activation reaches the threshold.
Commission: because of noise (explicit or implicit), the wrong fact has the highest activation.
Computation: the wrong answer is returned and becomes a fact.
Performance:
Problem Size Effect
Larger problems take longer and produce more errors.
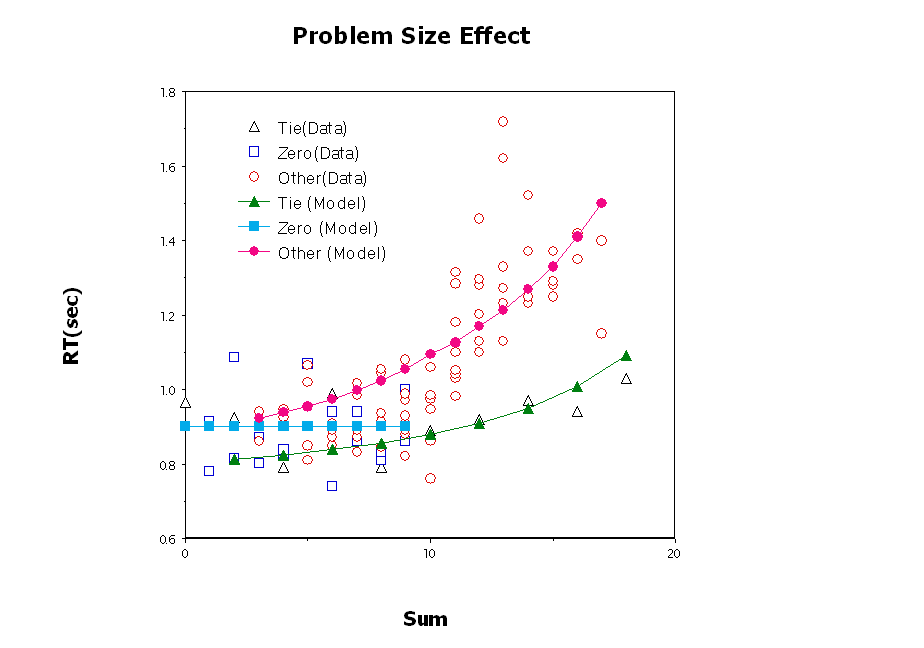
Models: computation vs retrieval-based
Assumption of frequency differential: external (presentation) vs internal (procedures) sources.
Standard prbms: base level and associative learning
Ties: associative boost
Reencoding strategies & independence assumption
Zeroes: proceduralized
Performance: Addition Retrieval (Data)
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | othr | ||
1+1 | 0 | 5 | 86 | 0 | 2 | 0 | 2 | 0 | 0 | 0 | 0 | 2 | 4 | |
1+2 | 0 | 0 | 9 | 70 | 2 | 0 | 4 | 0 | 0 | 7 | 2 | 2 | 5 | |
1+3 | 0 | 2 | 0 | 11 | 71 | 5 | 2 | 2 | 0 | 0 | 0 | 0 | 7 | |
1+4 | 0 | 0 | 0 | 0 | 11 | 61 | 9 | 7 | 0 | 0 | 0 | 2 | 11 | |
1+5 | 0 | 0 | 0 | 0 | 13 | 16 | 50 | 11 | 0 | 2 | 2 | 0 | 5 | |
2+1 | 0 | 7 | 5 | 79 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | |
2+2 | 2 | 0 | 4 | 5 | 80 | 4 | 0 | 5 | 0 | 0 | 0 | 0 | 0 | |
2+3 | 0 | 0 | 4 | 7 | 38 | 34 | 9 | 2 | 2 | 2 | 0 | 0 | 4 | |
2+4 | 0 | 2 | 0 | 7 | 2 | 43 | 29 | 7 | 7 | 0 | 0 | 0 | 4 | |
2+5 | 0 | 2 | 0 | 5 | 2 | 16 | 43 | 13 | 0 | 0 | 2 | 0 | 18 | |
3+1 | 0 | 2 | 0 | 9 | 79 | 4 | 0 | 4 | 0 | 0 | 0 | 0 | 4 | |
3+2 | 0 | 0 | 9 | 11 | 11 | 55 | 7 | 0 | 0 | 0 | 0 | 0 | 7 | |
3+3 | 4 | 0 | 0 | 5 | 21 | 9 | 48 | 0 | 2 | 2 | 2 | 0 | 7 | |
3+4 | 0 | 0 | 0 | 5 | 11 | 23 | 14 | 29 | 2 | 0 | 0 | 0 | 16 | |
3+5 | 0 | 0 | 0 | 7 | 0 | 13 | 23 | 14 | 18 | 0 | 5 | 0 | 20 | |
4+1 | 0 | 0 | 4 | 2 | 9 | 68 | 2 | 2 | 7 | 0 | 0 | 0 | 7 | |
4+2 | 0 | 0 | 7 | 9 | 0 | 20 | 36 | 13 | 7 | 0 | 2 | 0 | 7 | |
4+3 | 0 | 0 | 0 | 5 | 18 | 9 | 9 | 38 | 9 | 0 | 2 | 0 | 11 | |
4+4 | 4 | 0 | 0 | 2 | 2 | 29 | 7 | 7 | 34 | 0 | 4 | 0 | 13 | |
4+5 | 0 | 0 | 0 | 0 | 4 | 9 | 16 | 9 | 11 | 18 | 11 | 4 | 20 | |
5+1 | 0 | 0 | 4 | 0 | 4 | 7 | 71 | 4 | 4 | 0 | 4 | 0 | 4 | |
5+2 | 0 | 0 | 5 | 20 | 2 | 18 | 27 | 25 | 2 | 0 | 2 | 0 | 0 | |
5+3 | 0 | 0 | 2 | 11 | 9 | 18 | 5 | 16 | 23 | 0 | 5 | 0 | 11 | |
5+4 | 0 | 0 | 0 | 0 | 11 | 21 | 16 | 5 | 11 | 16 | 4 | 0 | 16 | |
5+5 | 4 | 0 | 0 | 0 | 0 | 7 | 25 | 11 | 2 | 4 | 34 | 4 | 11 |
Error percentage increase with size
Problems involving 1 have many fewer errors
Tie problems have fewer errors (e.g. 4+4 vs 5+3 or 3+5)
Problems with a first operand larger than the second have fewer errors than their symmetric counterpart
Erroneous answers tend to be smaller than the correct answer.
Performance: Addition Retrieval (Model)
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | othr | ||
1+1 | 0 | 0 | 93 | 6 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
1+2 | 0 | 0 | 22 | 68 | 8 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
1+3 | 0 | 0 | 16 | 14 | 65 | 4 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
1+4 | 0 | 0 | 11 | 10 | 9 | 65 | 2 | 0 | 0 | 0 | 0 | 0 | 2 | |
1+5 | 0 | 0 | 10 | 9 | 8 | 8 | 58 | 1 | 0 | 0 | 0 | 0 | 6 | |
2+1 | 0 | 0 | 16 | 77 | 6 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
2+2 | 0 | 0 | 0 | 28 | 69 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
2+3 | 0 | 0 | 1 | 23 | 33 | 37 | 3 | 0 | 0 | 0 | 0 | 0 | 2 | |
2+4 | 0 | 0 | 1 | 20 | 18 | 23 | 32 | 1 | 0 | 0 | 0 | 0 | 4 | |
2+5 | 0 | 0 | 1 | 20 | 18 | 8 | 20 | 21 | 1 | 0 | 0 | 0 | 12 | |
3+1 | 0 | 0 | 10 | 13 | 72 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
3+2 | 0 | 0 | 1 | 17 | 32 | 46 | 3 | 0 | 0 | 0 | 0 | 0 | 1 | |
3+3 | 0 | 0 | 0 | 1 | 25 | 17 | 55 | 1 | 0 | 0 | 0 | 0 | 1 | |
3+4 | 0 | 0 | 0 | 3 | 19 | 23 | 18 | 29 | 1 | 0 | 0 | 0 | 7 | |
3+5 | 0 | 0 | 0 | 3 | 18 | 12 | 21 | 7 | 18 | 0 | 0 | 0 | 20 | |
4+1 | 0 | 0 | 7 | 9 | 10 | 70 | 2 | 0 | 0 | 0 | 0 | 0 | 1 | |
4+2 | 0 | 0 | 1 | 14 | 14 | 28 | 39 | 1 | 0 | 0 | 0 | 0 | 3 | |
4+3 | 0 | 0 | 0 | 2 | 15 | 23 | 17 | 35 | 1 | 0 | 0 | 0 | 6 | |
4+4 | 0 | 0 | 0 | 0 | 1 | 28 | 15 | 14 | 39 | 0 | 0 | 0 | 3 | |
4+5 | 0 | 0 | 0 | 2 | 2 | 15 | 14 | 9 | 8 | 13 | 0 | 0 | 36 | |
5+1 | 0 | 0 | 6 | 8 | 8 | 8 | 66 | 1 | 0 | 0 | 0 | 0 | 4 | |
5+2 | 0 | 0 | 1 | 14 | 13 | 10 | 27 | 27 | 1 | 0 | 0 | 0 | 8 | |
5+3 | 0 | 0 | 0 | 2 | 14 | 10 | 23 | 9 | 24 | 0 | 0 | 0 | 16 | |
5+4 | 0 | 0 | 0 | 2 | 2 | 13 | 16 | 9 | 8 | 19 | 0 | 0 | 31 | |
5+5 | 0 | 0 | 0 | 0 | 0 | 0 | 33 | 11 | 12 | 9 | 17 | 0 | 17 |
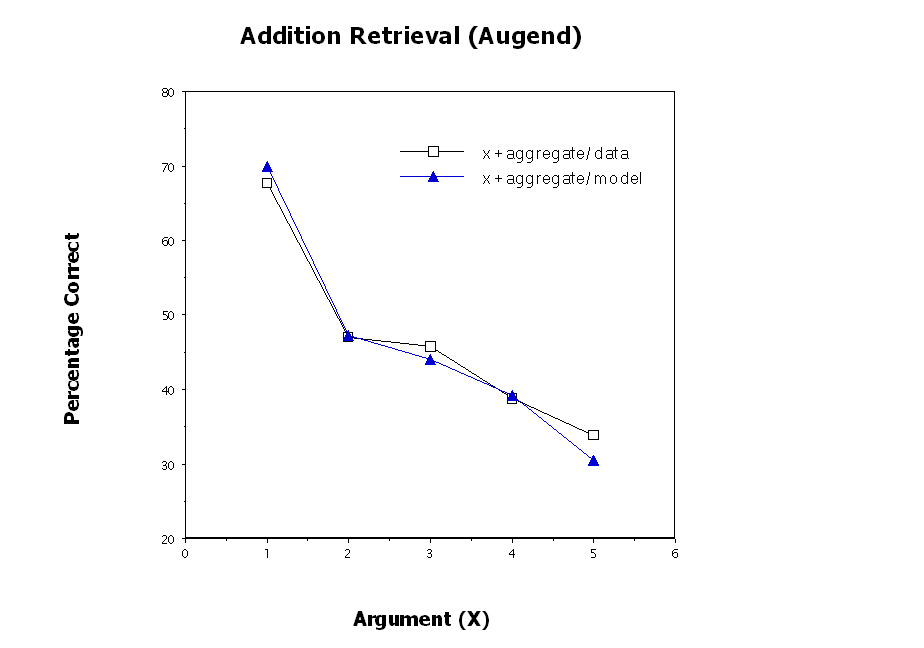
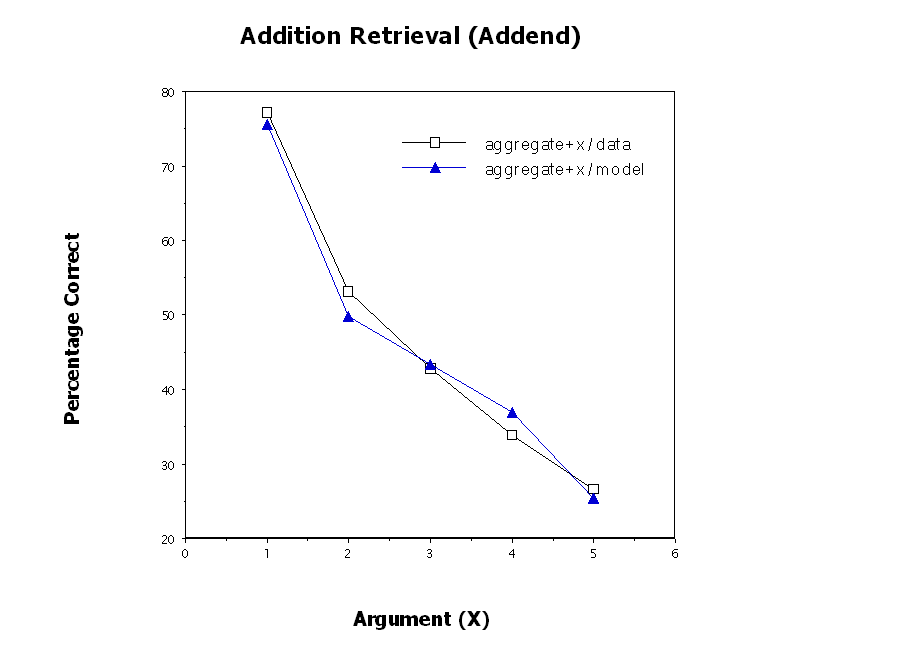
Larger problems have less activation and therefore are more likely to suffer from errors of commission
Facts involving 1 can leverage the strength of counting
Tie problems get extra activation boost
Backup strategies (counting errors, swap strategy) explain the argument asymmetry
Smaller problems are stronger, more likely to intrude
Performance: Addition Retrieval (Fit)
Performance: Multiplication by Repeated Addition
Errors increase with problem size.
Addition by 5s has very few errors.
|
|
Multiplier: linear increase in error percentage with number of opportunities
Multiplicand: smaller facts are stronger and lead to fewer errors
Addition by 5s: only two facts are used and reinforced
Errors are stored as facts and can later result in retrieval errors for multiplication in addition to table errors.
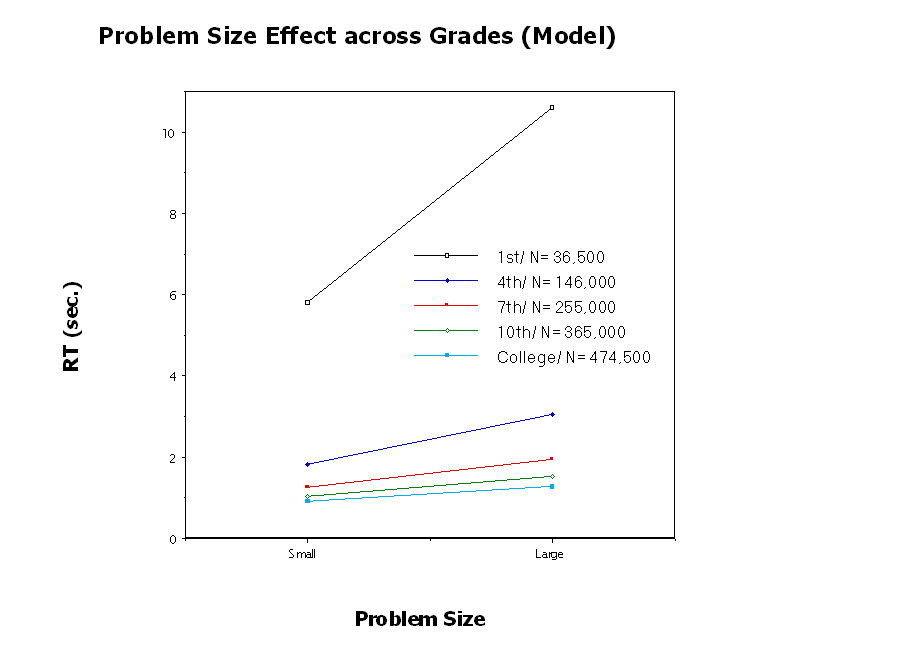
Learning: Problem Size Effect over Time
Latency and problem size effect decrease over time
The decrease approximates a power-law across grades
|
|
Combining the base-level and latency equations yields:
![]()
Assuming a presentation of 100 problems a day:
Learning: Cognitive Dynamics
The difference between the base-level activation of two memories reflects the ratio of their frequencies:
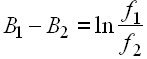
Assuming constant frequencies, this implies that practice does not affect differences in activations and thus commission errors!?
But while the environment may be fixed, performance and learning are a dynamic feedback loop. Performance, i.e. the retrieval odds, depends upon activation:
![]() Boltzmann Equation
Boltzmann Equation
and, since the activation difference reflects the log of the ratio of past rehearsals, the odds of retrieval are a function of the odds of past experience:
![]()
Through learning, these odds of retrieval then become part of the history. The behavior of the system then fundamentally depends upon the noise level s:
If s<1, the retrieval odds are more extreme than the past odds and the system becomes winner-take-all.
If s>1, the retrieval odds are less extreme than the past odds and all alternatives become equally likely.
If s=1, the retrieval odds reflect the past odds (probability matching) and the system drifts randomly with experience.
Learning: Cognitive Dynamics (Continued)
The impact of current odds of retrieval on past odds can be approximated by the differential equation:
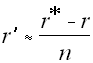
For values of s>1, this equation admits the approximate solutions for the odds of each memory:
![]()
The (observable) odds of retrieval can then be expressed as a power function of practice n to the inverse of the noise s:
![]()
Alternatively, the amount of practice needed to bring the odds of error (assuming that the correct solution emerges) below some threshold ![]() is:
is:
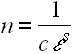
The power function is a very widespread transition function between stable points in a physical system.
Learning: Cognitive Dynamics (Results)
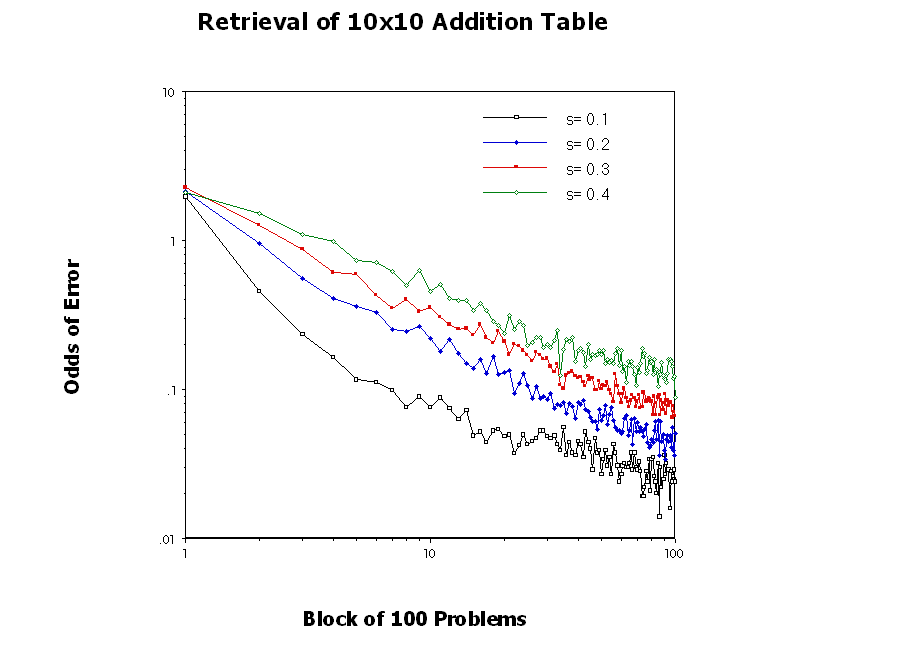
Large differences in convergence time can be explained by small differences in initial performance.
The noise slows down convergence but can keep an error from locking in early, which suggests a role similar to the temperature in simulated annealing and reflects the changing and uncertain nature of the environment in which human cognition evolved.
Learning: Influence of Various Factors
Context: add spreading activation to frequency-based base level. The analysis still works, but the complexity of the context, i.e. the number of sources, acts as a noise multiplier because only one source may separate it from its competing neighbors, i.e the three sources of arithmetic facts effectively triple the noise.
Partial matching: the mismatch penalty improves the performance by a constant factor of ![]() but does not affect the speed of convergence.
but does not affect the speed of convergence.
Multiple alternatives: the odds of any one choice reflects the (harmonic) average of each pairwise odds (Luces choice axiom), which slows down the emergence of the ultimate winner.
External feedback sources: feedback reinforces the retrieval odds of the correct answer by the feedback probability. This underscores the importance of early teaching, before odds have grown much larger than probabilities. It also raises the question of the impact of transient strenghening on long-term learning.
The Lifetime Simulation
Goal: extend the simulation beyond static models to a dynamic model of lifetime arithmetic performance and learning from childhood to adulthood.
Learning needs to proceed at the symbolic and subsymbolic level:
Goals become facts
Facts become strengthened (base-level and associative connections) with experience
Productions are analogized from examples
Productions are strengthened with experience
The evaluation of the utility of productions is refined, leading to shifts in strategy
Concurrently, the formal analysis will be extended from a single retrieval process to reflect the dynamic interaction between a number of processes for each skill (counting, addition, multiplication) and procedure (retrieval, iterative computation, etc).
Conclusion
Cognitive arithmetic can be effectively modeled using the Bayesian learning mechanisms for the subsymbolic parameters associated with the symbolic knowledge structures resulting from instructional material and problem-solving experience.
Further, the behavior of the resulting system can best be understood not only in terms of modeling the statistics of the environment, but also as emerging from the interactions between the components of the system, which each impose an additional set of internal statistics upon the knowledge modules with which it competes or interacts.